Horário de Atendimento
- Em qualquer altura: via correio electrónico pressionando aqui. Qualquer outro meio de contacto será considerado informal, não se sentindo a equipa docente vinculada a dar uma resposta em tempo útil.
- Durante o período de aulas: de acordo com o horário seguinte, sujeito a marcação verbal ou por email, com um mínimo de uma semana de antecedência, junto do respectivo docente:
| Dia | Hora | Cursos | Docente |
|---|---|---|---|
| 5.ª-feira | 10h00-11h00 | MiEI | H. Pacheco |
| 3.ª-feira | 11h00-12h00 | LCC | J.M. Proença |
| 2.ª-feira | 19h00-20h00 | MiEI | J.N. Oliveira |
| 6.ª-feira | 18h00-19h00 | LCC | J.N. Oliveira |
| 6.ª-feira | 19h00-20h00 | MiEI | J.N. Oliveira |
| 3.ª-feira | 11h00-12h00 | MiEI/LCC | R. Neves |
Atendimento electrónico (FAQs) 
Q01 - Ao compilar o trabalho deparámo-nos com o erro
Q02 - Não consigo definir funções com o padrão (n+1). O que devo fazer? R: Há duas soluções: ou adiciona {-# OPTIONS_GHC -XNPlusKPatterns #-} no início do código Haskell em cp1617t.lhs, ou interpreta o ficheiro como essa opção passada como parâmetro,
Q03 - No Problema 2 escreve-se que o "wrapper deverá ser um catamorfismo". O catamorfismo não deveria ser o "worker" e não o "wrapper"? R: Sim! É uma gralha: nesse texto, onde está "wrapper" deve ler-se "worker" (ver correcção feita sobre o PDF).
Q04 - No Problema 2 é obrigatório usar a lei de recursividade múltipla? R: Se se recomenda usá-la é porque é a melhor alternativa. Não se esqueçam que têm de apresentar os cálculos justificativos de como chegaram à vossa solução.
Q05 - No Problema 2 é pedido para apresentarmos os cálculos. O que é preciso fazer no LaTeX para reproduzir o "layout" dos raciocínios que aparecem nas fichas e nos apontamentos? R: Fazem assim: (a) ao ficheiro cp1617t.sty acrescentam, em qualquer sítio, as linhas
\def\start{&&}
\def\just#1#2{\\ & \rule{2em}{0pt} \{ \mbox{\rule[-.7em]{0pt}{1.8em} \small #2 \/} \} \nonumber\\ && }
(b) depois usam o esquema ilustrado a seguir (adaptado da Ficha 5):
\begin{eqnarray*}
\start
|p? . f|
%
\just={ justificação ..... }
%
|alpha.(split (p.f) f)|
%
\just={ justificação ..... }
%
|alpha.(id >< f).(split (p.f) id)|
%
---- etc -----
%
\end{eqnarray*}
Q06 - Não percebemos o funcionamento da função 'lsplitB_tree'. Como é que a decisão sobre quantos elementos ficam na raiz, e.g., é tomada? E depois como são inseridos os restantes elementos? R: A função lsplitB_tree está para B_tree assim como qsep está para BTree (ver BTree.hs). Neste caso, só é possível guardar um valor em cada nó da árvore gerada, enquanto que em B_tree se pode guardar mais do que um. Portanto, em vez de se gerar uma BTree de procura, pode gerar-se uma B_tree de procura, com várias sub-árvores em cada nó e obter um 'quicksort' mais interessante. Dá-se de seguida um exemplo que pode ajudar: o anamorfismo com gene lsplitB_tree aplicado à lista [7,16,5,6,12,9,21,18] deverá dar a árvore intermédia que a seguir se representa:
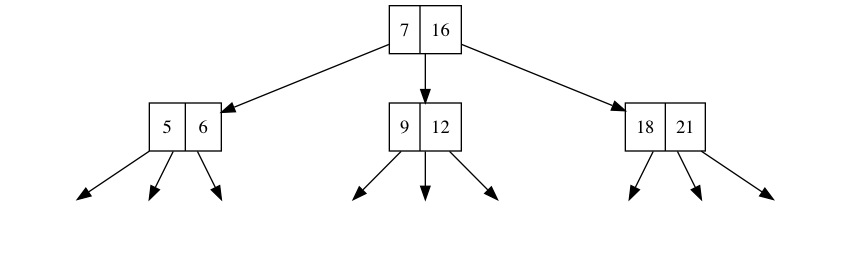
Q07 - Há alguma maneira de testarmos se a nossa função 'mirrorB_tree' está bem implementada? R: Naturalmente que essa função deve ser inversa de si própria. Outra forma de a verificarem é fazerem o seguinte teste, quando o problema estiver acabado. Como sabem, qSort = cataBTree inord . anaBTree qsep. no módulo BTree.hs. Se no meio do algoritmo colocarem invBTree a lista de entrada virá ordenada por ordem inversa. Ora invBTree corresponde à vossa mirrorB_tree. Assim, se ao adaptarem este teste ao vosso quicksort sobre B_tree a lista de entrada não aparecer por ordem inversa, então a vossa mirrorB_tree não está a funcionar bem.
Q08
 - Há alguma convenção uma para os testes quickCheck?
R: O enunciado é omisso quanto a este ponto. No entanto, dá jeito que as funções quickcheck tenham o prefixo prop_XXX (desde que quickCheck prop_XXX tipe correctamente).
- Há alguma convenção uma para os testes quickCheck?
R: O enunciado é omisso quanto a este ponto. No entanto, dá jeito que as funções quickcheck tenham o prefixo prop_XXX (desde que quickCheck prop_XXX tipe correctamente).
Q9
 - Na alínea 4(c) da ficha nº 6, fiz os diagramas de cada catamorfismo e chego às definições das funções com variáveis através da lei universal-cata e consigo perceber que realmente fazem a mesma coisa; mas não sei se era assim que era suposto resolver...
R: Não: isso mostra, mas não prova! O que queremos provar é que f=g, sendo ambas catamorfismos. Logo podemos usar a lei-universal aplicada a f ou g, à nossa escolha, por exemplo
- Na alínea 4(c) da ficha nº 6, fiz os diagramas de cada catamorfismo e chego às definições das funções com variáveis através da lei universal-cata e consigo perceber que realmente fazem a mesma coisa; mas não sei se era assim que era suposto resolver...
R: Não: isso mostra, mas não prova! O que queremos provar é que f=g, sendo ambas catamorfismos. Logo podemos usar a lei-universal aplicada a f ou g, à nossa escolha, por exemplo
Q10 - Na questão nrº 5 da ficha 9, no terceiro passo, eu passei 'out' para o outro lado da igualdade,
Q11 - Pretendemos desenhar diagramas de catamorfismos como aparecem nos apontamentos e nas fichas. O que temos de fazer? R: A package LaTeX para fazerem isso carrega-se adicionando
\usepackage[all]{xy}
ao preâmbulo. Há um extenso manual sobre esta package fácil de encontrar.
Fica disponível a função \xymatrix que é usada a seguir para desenhar um dos diagramas da ficha 6:
\xymatrix@@C=2cm{
|Nat|
\ar[d]_-{|cata g|}
&
|1 + Nat0|
\ar[d]^{|id + (cata g)|}
\ar[l]_-{|inNat|}
\\
|B|
&
|1 + B|
\ar[l]^-{|g|}
}
Agora é só adaptar ao caso concreto que querem desenhar.
Q12 - Qual é o formato em que apenas uma chaveta abrange duas equações, para colocar por exemplo o passo de passagem da lei de recursividade múltipla? R: Acrescentem ao preâmbulo as linhas
%format (lcbr (x)(y)) = "\begin{lcbr}" x "\\" y "\end{lcbr}"
\newenvironment{lcbr}{\left\{\begin{array}{l}}{\end{array}\right.}
Exemplo: |lcbr (id= g.f)(f.g=id)| na ficha 4.
Q13 - A utilização da função succ sem a aplicar a nenhuma variável resulta, em alguns contextos, num erro de geração do PDF. R: Isso deve-se ao facto de \succ no ficheiro auxiliar cp1617t.sty (linha 58) estar definido com um parâmetro. Sugere-se a re-definição (local)
%format succ = "\mathsf{succ}"
Q14
 - Ao escrever as justificações tenho erros em, por exemplo, \just<=>{ texto }. Qual é o problema?
R: Isso deve-se a <=> ser código Haskell e não código LaTeX. Resolve-se o erro escrevendo \just{|<=>|}{ texto }.
- Ao escrever as justificações tenho erros em, por exemplo, \just<=>{ texto }. Qual é o problema?
R: Isso deve-se a <=> ser código Haskell e não código LaTeX. Resolve-se o erro escrevendo \just{|<=>|}{ texto }.
Q15
 - Em relação à FAQ 12, funciona mas diz que o ambiente já está definido...
R: Têm razão - a linha
- Em relação à FAQ 12, funciona mas diz que o ambiente já está definido...
R: Têm razão - a linha
\newenvironment{lcbr}{\left\{\begin{array}{l}}{\end{array}\right.}
já existe em cp1617t.sty; logo não faz falta.
Q16
 - Nas justificações do problema 2 temos expressões muito grandes que saem fora da página. Como podemos resolver isso?
R: Sugiro que usem algo do género
- Nas justificações do problema 2 temos expressões muito grandes que saem fora da página. Como podemos resolver isso?
R: Sugiro que usem algo do género
%format (longcond (c)(t)(e)) =
"\begin{array}{ll}\multicolumn{2}{l}{" c -> "}\\& " t ",\\& " e "\end{array}"
que divide um condicional em três linhas. (O texto acima todo numa linha: está partido em duas para o html não cortar o que não pode mostrar.)
Q17
 - Ao justificarmos a recursividade multipla há 2 equações que, quando nelas introduzimos variáveis, acabamos com 4 equações. O que se sugere na FAQ 12 só dá para duas, como resolver este caso?
R: Sugerem-se dois lcbr dentro de um lcbr (2 * 2 = 4).
- Ao justificarmos a recursividade multipla há 2 equações que, quando nelas introduzimos variáveis, acabamos com 4 equações. O que se sugere na FAQ 12 só dá para duas, como resolver este caso?
R: Sugerem-se dois lcbr dentro de um lcbr (2 * 2 = 4).